Fork me on GitHub

数据结构之红黑树

发表于 | 分类于 | |
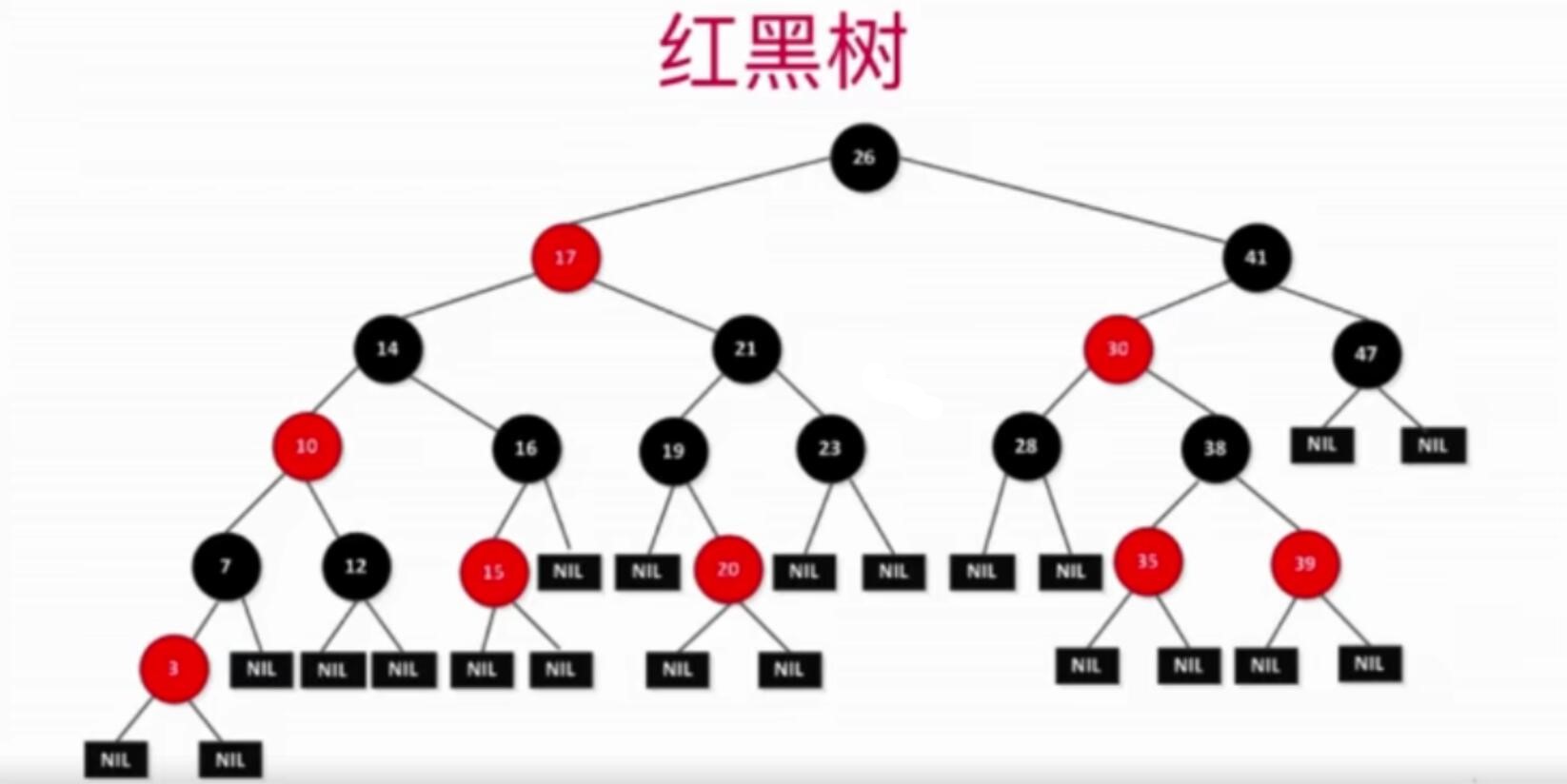
红黑树是什么

《算法导论》中的红黑树

  1. Every node is either red or black.
  2. The root is black.
  3. Every leaf(NIL) is black.
  4. If a node is red ,then both its children are black.

  5. For each node,all simple paths from the node to descendant leaves contain the same number of black nodes.

  6. 每个节点或者是红色的，或者是黑色的

  7. 根节点是黑色的
  8. 每个叶子节点（最后的空节点）是黑色的
  9. 如果一个节点是红色的，那么他的孩子节点都是黑色的
  10. 从任意一个节点到叶子节点，经过的黑色节点是一样的

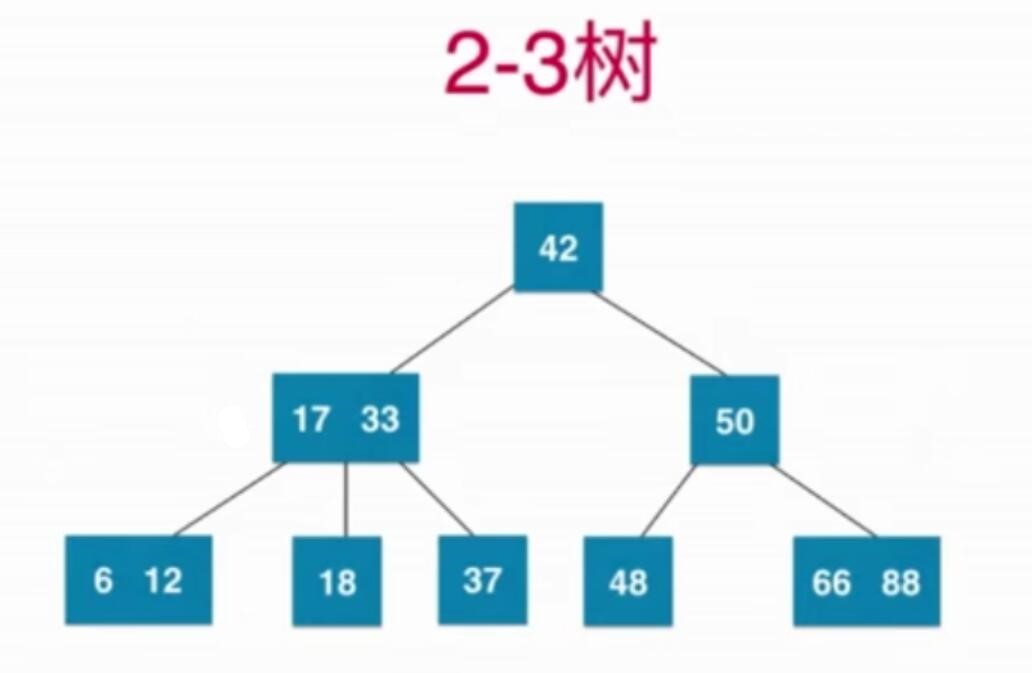
2-3树

2-3树也是平衡二叉树,2-3是一棵绝对平衡的树，对于任意一个节点，高度绝对相等

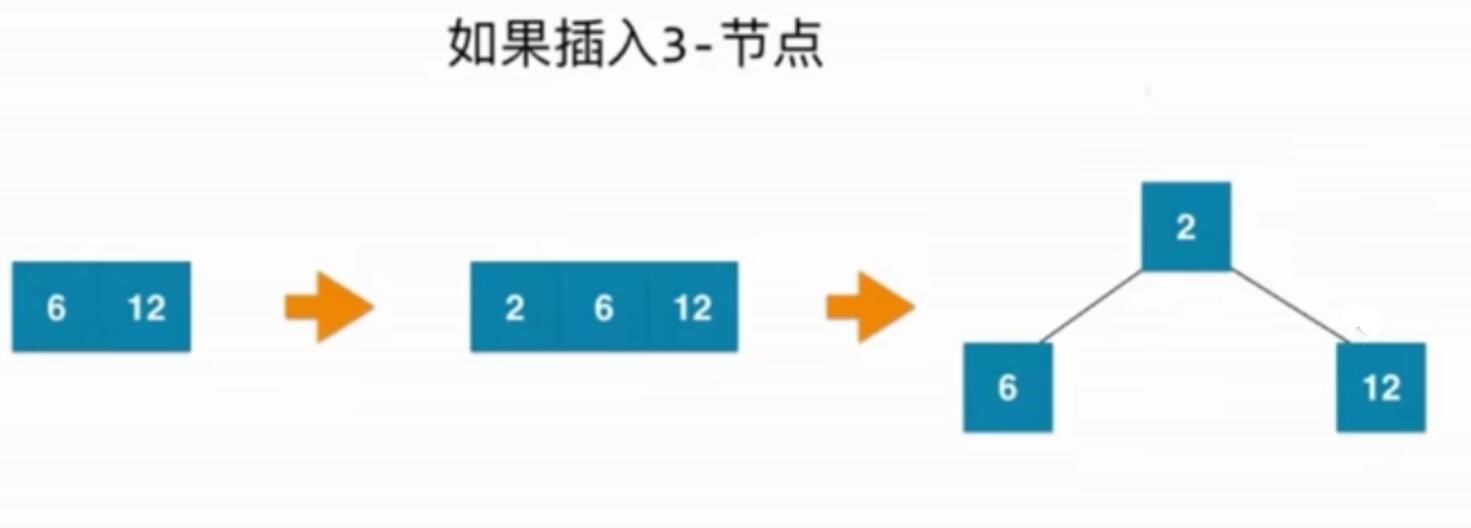
2-3树如何维持绝对的平衡

如果插入2节点

如果插入3节点

如果插入3节点 父亲节点为2节点

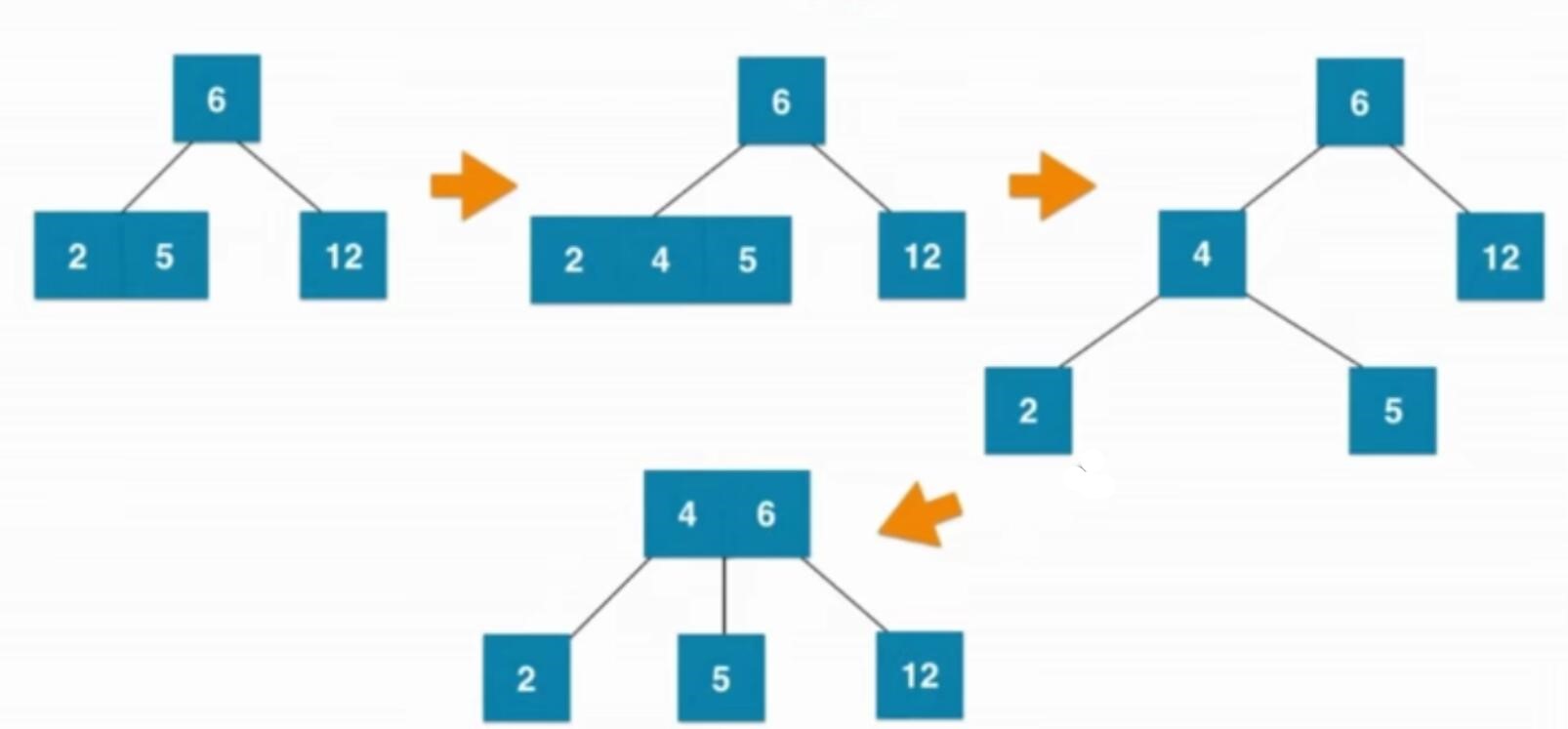
如果插入3节点 父亲节点为3节点

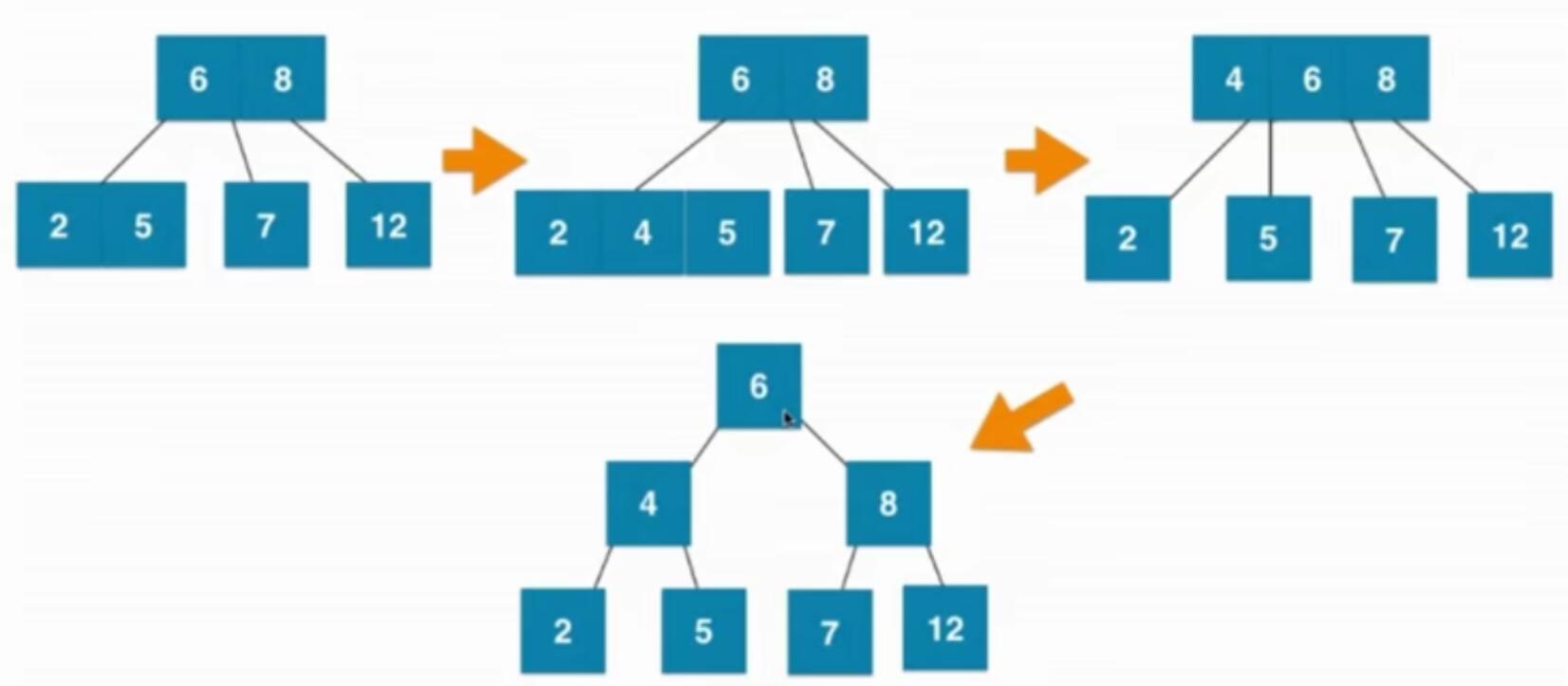
红黑树和2-3树

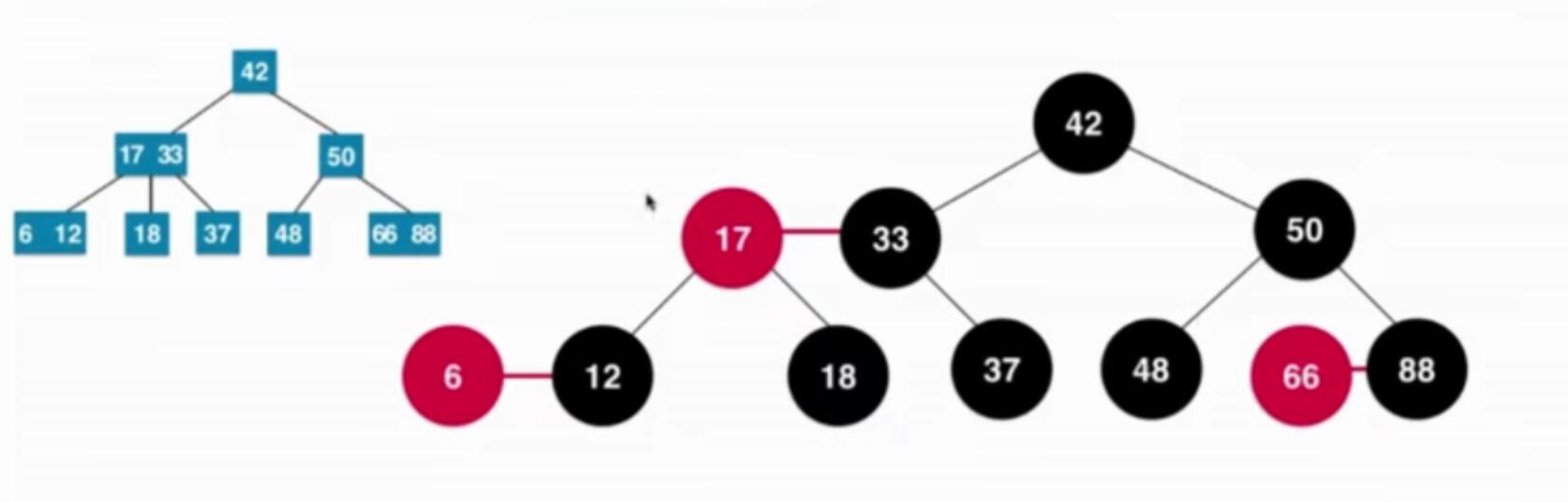
红黑树是保持黑平衡的二叉树，严格意义上，不是平衡二叉树，最大高度： O（logn）

左旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//    node                          x
   //   /    \     左旋转            /    \
   //  T1     x  -------------->   node    T3
   //        /   \                /    \
   //        T2   T3             T1     T2
   //
   //
   private Node leftRotate(Node node)
   {
       Node x = node.right;

       //左旋转
       node.right=x.left;
       x.left = node;

       x.color = node.color;
       node.color = RED;

       return x;
   }

右旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//      node                        x
  //     /    \     右旋转           /  \
  //    x      T2 ------------>     y     node
  //   /  \                              /    \
  //  y    T1                           T1     T2
  //
  //
  //
  private Node rightRotate(Node node)
  {
      Node x = node.left;

      //右旋转
      node.left = x.right;
      x.right = node;

      x.color = node.color;
      node.color = RED;
      return x;
  }

颜色反转

1
2
3
4
5
6
7
//颜色反转
    private void filpColors(Node node)
    {
        node.color = RED;
        node.left.color = BLACK;
        node.right.color = BLACK;
    }
红黑树的性能总结
  • 对于完全随机的数据，普通的二分搜索树很好用，缺点，极端情况退化成链表（或者高度不平衡）
  • 对于查询较多的使用情况，AVL树很好用
  • 红黑树牺牲了平衡性（2logn），统计性能更优（综合增删改查所有的操作）