数据结构之平衡二叉树与AVL树

平衡二叉树

由于二分搜索树顺序创建一个树时，会退化成链表，大大降低的效率，我们引出平衡二叉树——AVL树，G.M.Adelson-Velsky和E.M.Landis ，AVL，最早的自平衡二分搜索树结构。

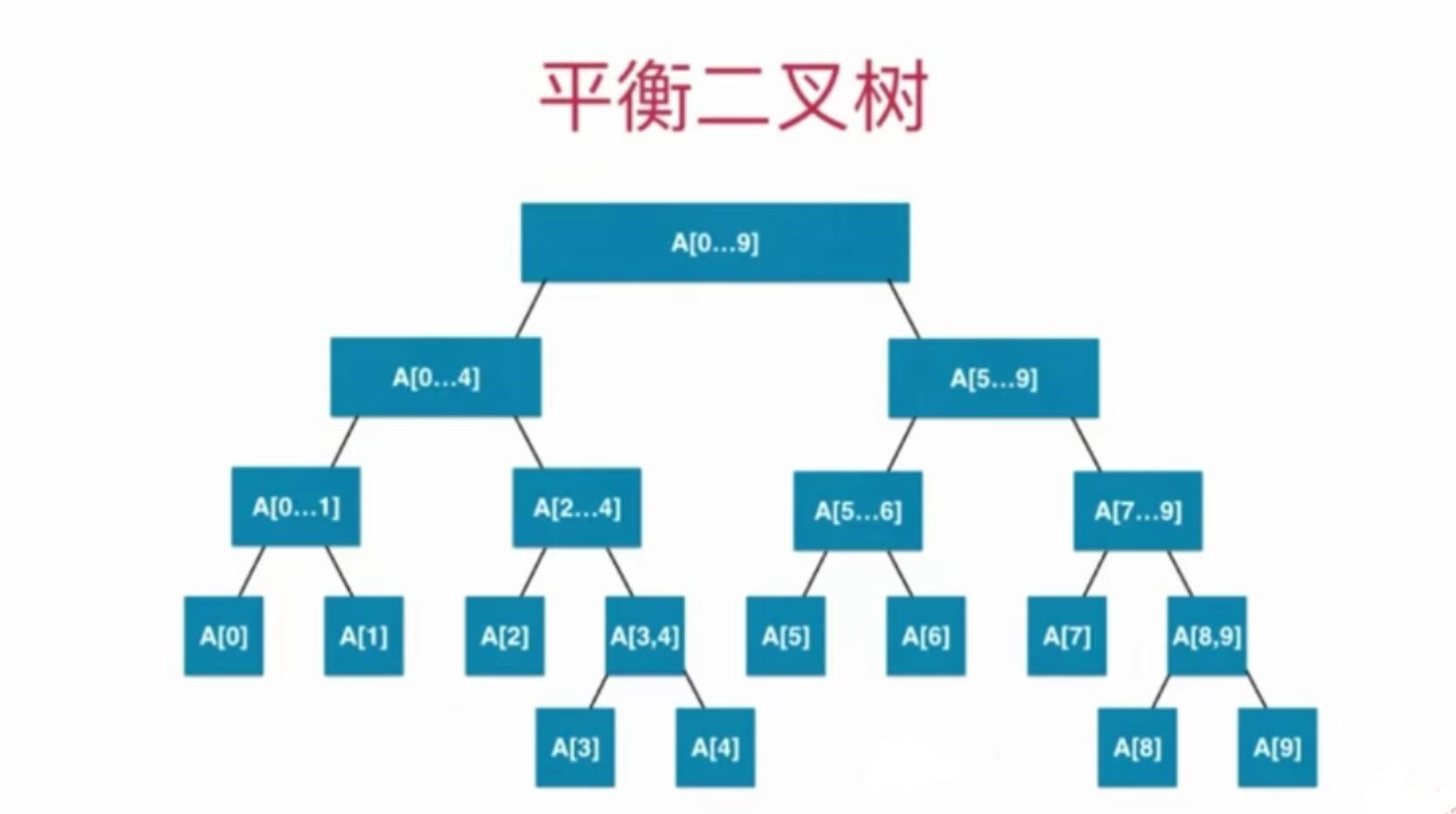
平衡二叉树特点

• 对于任意一个节点，左子树和右子树的高度查不能为超过1
• 平衡二叉树的高度和节点数量之间的关系也是O（logn）的
• 节点高度
• 平衡因子

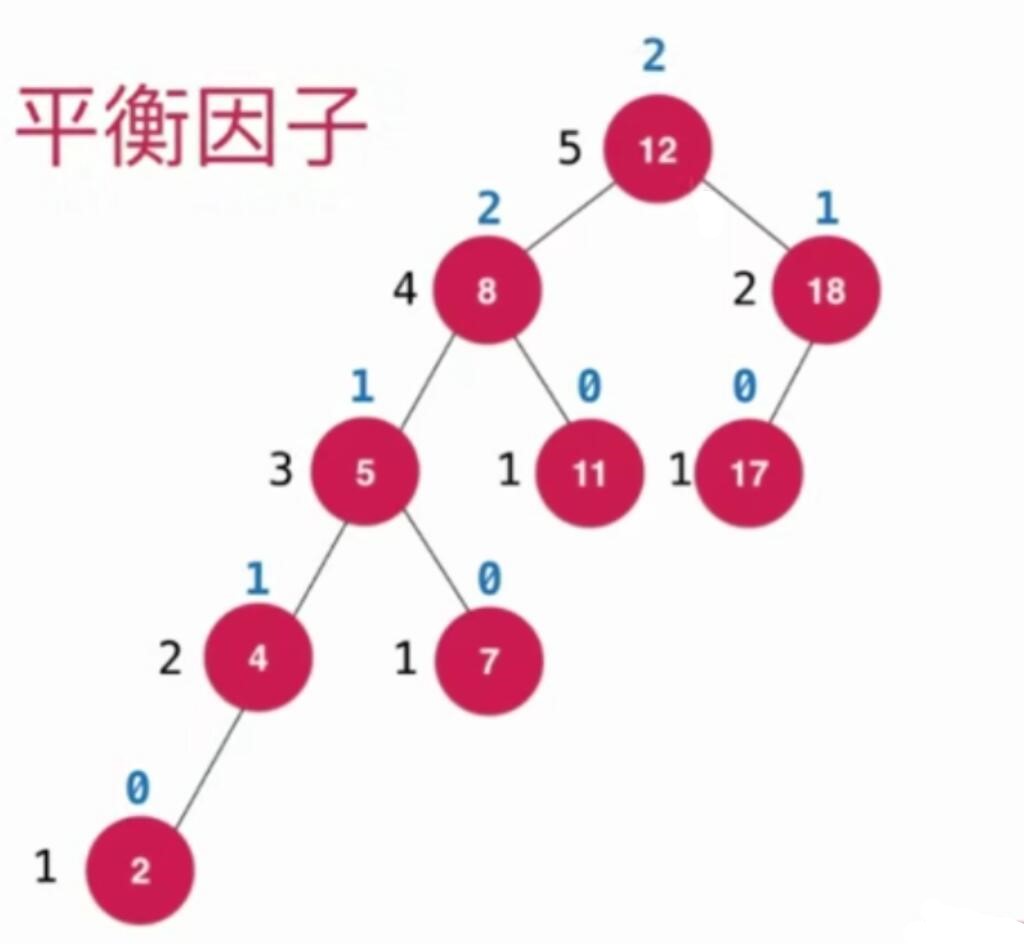
AVL树的增删

package AVL;

import java.lang.reflect.Array;
import java.util.ArrayList;

/**
 * @author zqnh
 * @date 2019/8/4 on 10:44.
 */
public class AVLTree<K extends Comparable<K>,V>
{
    private class Node
    {
        public K key;
        public V value;
        public Node left,right;
        public int height;
        public Node(K key,V value)
        {
            this.key=key;
            this.value = value;
            left=null;
            right=null;
            height=1;
        }
    }

    private Node root;
    private int size;
    public AVLTree()
    {
        root=null;
        size=0;
    }
    //获得节点node的高度
    private int getHeight(Node node)
    {
        if(node == null)
            return 0;
        return node.height;
    }

    //获得节点node的平衡因子
    private int getBalanceFactor(Node node)
    {
        if(node == null)
            return 0;
        return getHeight(node.left) - getHeight(node.right);
    }
    //对节点进行右旋操作，返回旋转后新的根结点x
    //          y                            x
    //         / \                         /   \
    //        x         向右旋转（y）      z      y
    //       / \    ---------------->   /   \   /   \
    //      z   T3                     T1   T2  T3   T3
    //     / \
    //    T1  T2
    private Node rightRotate(Node y)
    {
        Node x = y.left;
        Node T3 = x.right;

        //向右旋转
        x.right = y;
        y.left = T3;

        //更新height
        y.height = Math.max(getHeight(y.left),getHeight((y.right)) + 1 );
        x.height = Math.max(getHeight(x.left),getHeight((x.right)) + 1 );

        return x;
    }
    //对节点y进行左旋转操作，返回旋转后新的根结点x
    //     y                                    X
    //    / \                                 /   \
    //  T1    x     向左旋转（y）             Y     z
    //       / \ ----------------------->  / \    / \
    //      T2  z                         T1   T2 T3  T4
    //          / \
    //         T3  T4
    private Node leftRotate(Node y)
    {
        Node x = y.right;
        Node T2 = x.left;

        //向左旋转
        x.left = y;
        y.right = T2;

        //更新height
        y.height = Math.max(getHeight(y.left),getHeight((y.right)) + 1 );
        x.height = Math.max(getHeight(x.left),getHeight((x.right)) + 1 );

        return x;
    }


    public void add(K key, V value)
    {
        root = add(root, key,value);
    }
    private Node add(Node node,K key,V value)
    {
        if(node == null)
        {
            size++;
            return new Node(key,value);
        }
        if(key.compareTo(node.key)<0)

            node.left = add(node.left,key,value);
        else if (key.compareTo(node.key) > 0 )
            node.right = add(node.right,key,value);
        else
            node.value = value;
        //更新height
        node.height = 1+Math.max(getHeight(node.left),getHeight(node.right));
        //计算平衡因子
        int balanceFactor = getBalanceFactor(node);
        if(Math.abs(balanceFactor)>1) System.out.println(balanceFactor);
        //平衡维护
        //LL
        if(balanceFactor>1&&getBalanceFactor(node.left)>=0)
            return rightRotate(node);
        //RR
        if(balanceFactor<-1&& getBalanceFactor(node.right)<=0)
            return leftRotate(node);
        //LR
        if(balanceFactor>1&&getBalanceFactor(node.left)<0)
        {
            node.left = leftRotate(node.left);//转化为LL型
            return rightRotate(node);
        }
        //RL
        if(balanceFactor<-1&&getBalanceFactor(node.right)>0)
        {
            node.right = rightRotate(node.right);//转化为LL型
            return leftRotate(node);
        }
        return node;
    }


    public V remove(K key)
    {
        Node node = getNode(root,key);
        if(node!=null)
        {
            root = remove(root,key);
            return node.value;
        }
        return null;
    }
    //删除掉以node为根的二分搜索树中键为key的结点，递归算法
    //返回删除结点后新的二分搜索树的根
    private Node remove(Node node, K key)
    {
        if(node == null)
            return null;
        Node retNode;
        if(key.compareTo(node.key)<0)
        {
            node.left = remove(node.left,key);
            retNode =  node;
        }
        else if(key.compareTo(node.key)>0)
        {
            node.right = remove(node.right,key);
            retNode =  node;
        }
        else
        {//e == node.e
            //待删除结点左子树为空的情况
            if(node.left == null)
            {
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            }
            //待删除结点右子树为空的情况
           else if(node.right == null)
            {
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode =  leftNode;
            }
           else
               { //待删除结点左右子树均不为空的情况
                //找到比待删除结点大的最小结点，即待删除结点右子树的最小结点
                //用这个结点顶替待删除结点的位置
                Node successor = minimum(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;

                node.left = node.right = null;

                retNode = successor;
             }
        }

        if(retNode == null)
            return null;
        //更新height
        retNode.height = 1+Math.max(getHeight(retNode.left),getHeight(retNode.right));
        //计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);
        if(Math.abs(balanceFactor)>1) System.out.println(balanceFactor);
        //平衡维护
        //LL
        if(balanceFactor>1&&getBalanceFactor(retNode.left)>=0)
            return rightRotate(retNode);
        //RR
        if(balanceFactor<-1&& getBalanceFactor(retNode.right)<=0)
            return leftRotate(retNode);
        //LR
        if(balanceFactor>1&&getBalanceFactor(retNode.left)<0)
        {
            retNode.left = leftRotate(retNode.left);//转化为LL型
            return rightRotate(retNode);
        }
        //RL
        if(balanceFactor<-1&&getBalanceFactor(retNode.right)>0)
        {
            retNode.right = rightRotate(retNode.right);//转化为LL型
            return leftRotate(retNode);
        }
        return retNode;
    }
    private Node minimum(Node node)
    {
        if(node.left == null)
            return node;
        return minimum(node.left);
    }

    public boolean contains(K key)
    {
        return getNode(root,key)!=null;
    }


    public V get(K key)
    {
        Node node = getNode(root,key);
        return node == null?null:node.value;
    }


    public void set(K key, V newValue)
    {
        Node node = getNode(root,key);
        if(node == null)
            throw new IllegalArgumentException(key+"doesn't exist");
        node.value= newValue;
    }

    public int getSize()
    {
        return size;
    }


    public boolean isEmpty()
    {
        return size==0;
    }

    //判断该二叉树是否是一棵二分搜索树
    public boolean isBST()
    {
        ArrayList<K> keys = new ArrayList<>();
        inOrder(root,keys);
        for (int i = 0; i < keys.size(); i++) {
            if(keys.get(i-1).compareTo(keys.get(i))>0)
                return false;

        }return true;
    }
    //判断该二叉树是否是一颗平衡二叉树
    public boolean isBalanced()
    {
        return isBalanced(root);
    }
    private boolean isBalanced(Node node)
    {
        if(node ==null)
            return true;
        int balanceFactor = getBalanceFactor(node);

        if(Math.abs(balanceFactor)>1)
            return false;
        return isBalanced(node.left) && isBalanced(node.right);
    }

    private void inOrder(Node node, ArrayList<K> keys)
    {
        if(node == null )
        return;
        inOrder(node.left,keys);
        keys.add(node.key);
        inOrder(node.right,keys);
    }
    private Node getNode(Node node,K key)
    {
        if(node == null)
            return null;
        if(key.compareTo(node.key) == 0)
            return node;
        else if(key.compareTo(node.key)<0)
            return getNode(node.left,key);
        else
            return getNode(node.right,key);
    }
}

AVL树的左旋和右旋

//对节点进行右旋操作，返回旋转后新的根结点x
  //          y                            x
  //         / \                         /   \
  //        x         向右旋转（y）      z      y
  //       / \    ---------------->   /   \   /   \
  //      z   T3                     T1   T2  T3   T3
  //     / \
  //    T1  T2
  private Node rightRotate(Node y)
  {
      Node x = y.right;
      Node T3 = x.right;
      //向右旋转
      x.right = y;
      y.left = T3;

      //更新height
      y.height = Math.max(getHeight(y.left),getHeight((y.right)) + 1 );
      x.height = Math.max(getHeight(x.left),getHeight((x.right)) + 1 );

      return x;
  }

//对节点y进行左旋转操作，返回旋转后新的根结点x
   //     y                                    X
   //    / \                                 /   \
   //  T1    x     向左旋转（y）             Y     z
   //       / \ ----------------------->  / \    / \
   //      T2  z                         T1   T2 T3  T4
   //          / \
   //         T3  T4
   private Node leftRotate(Node y)
   {
       Node x = y.right;
       Node T2 = x.left;

       //向左旋转
       x.left = y;
       y.right = T2;

       //更新height
       y.height = Math.max(getHeight(y.left),getHeight((y.right)) + 1 );
       x.height = Math.max(getHeight(x.left),getHeight((x.right)) + 1 );

       return x;
   }

LL RR LR RL

左左型，右右型，左右型，右左型

LR

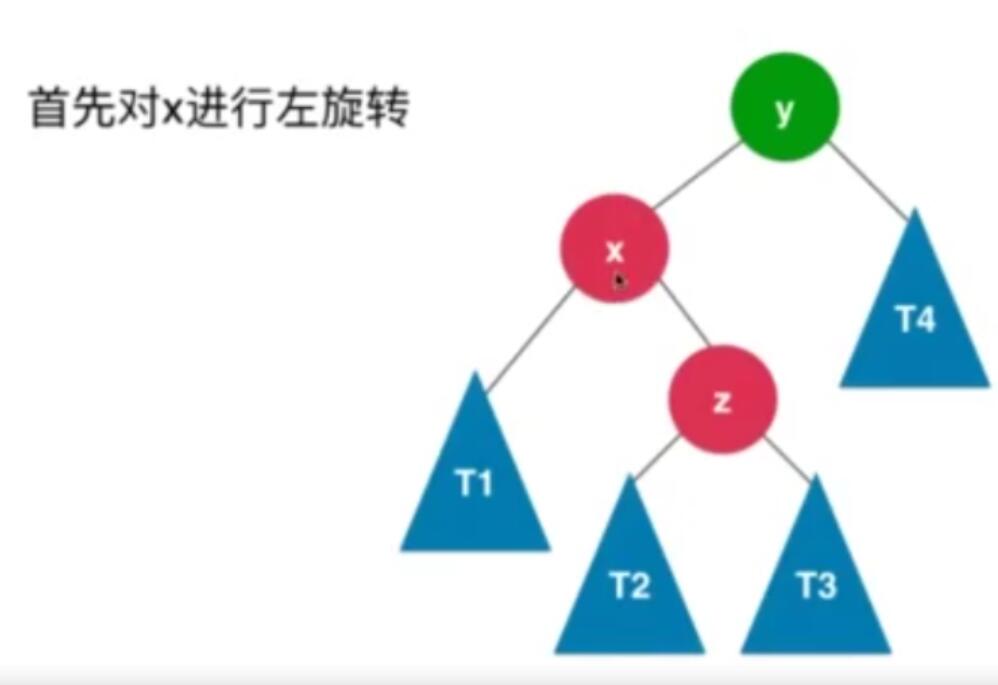
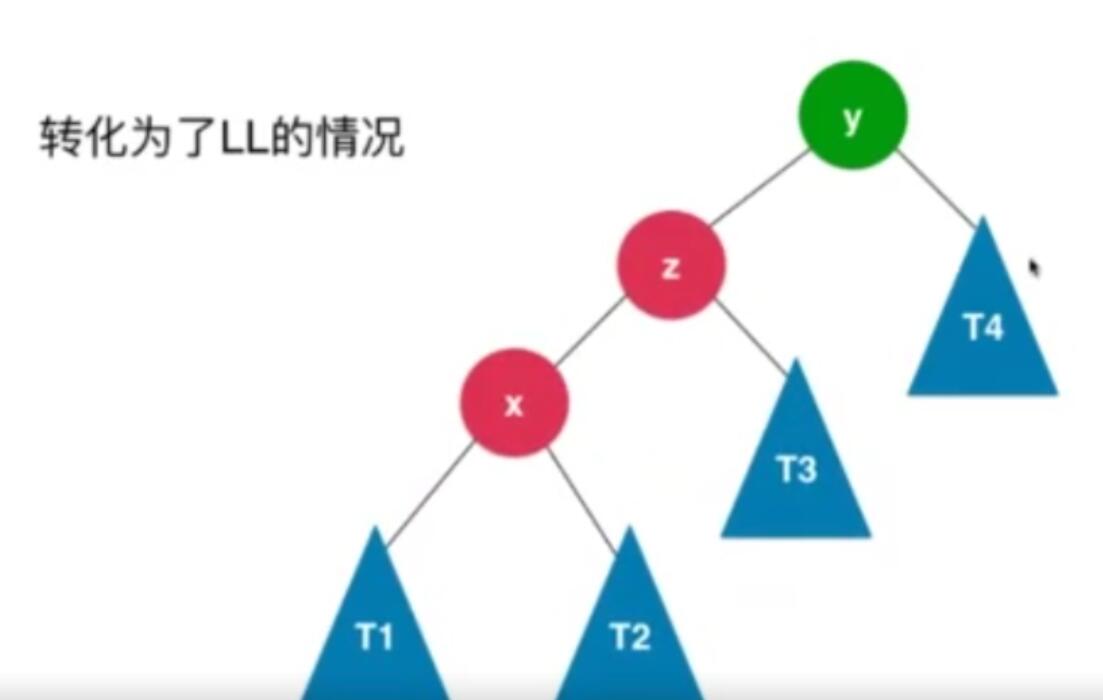
然后再对树进行右旋

---

RL

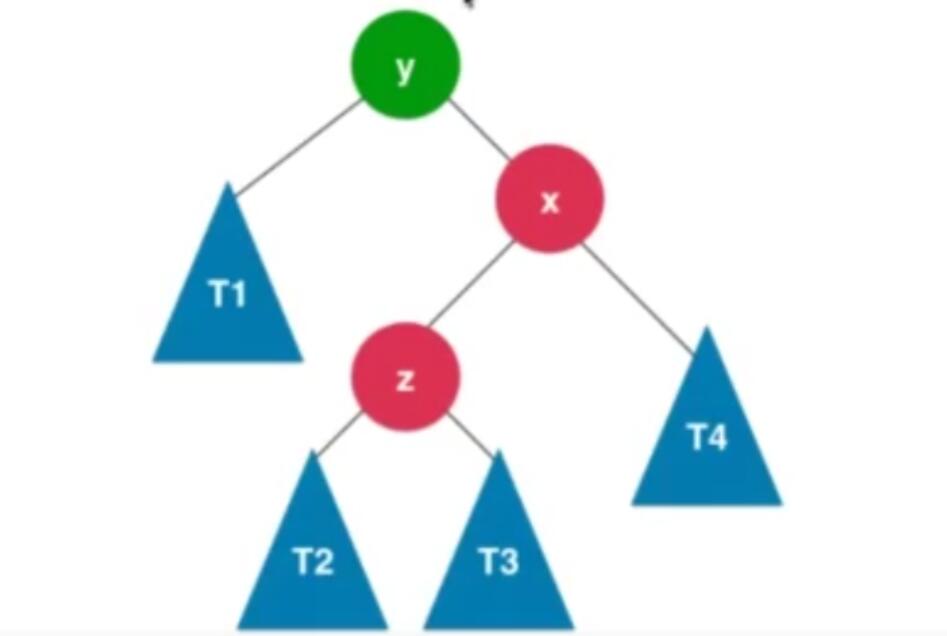
对x进行右旋转

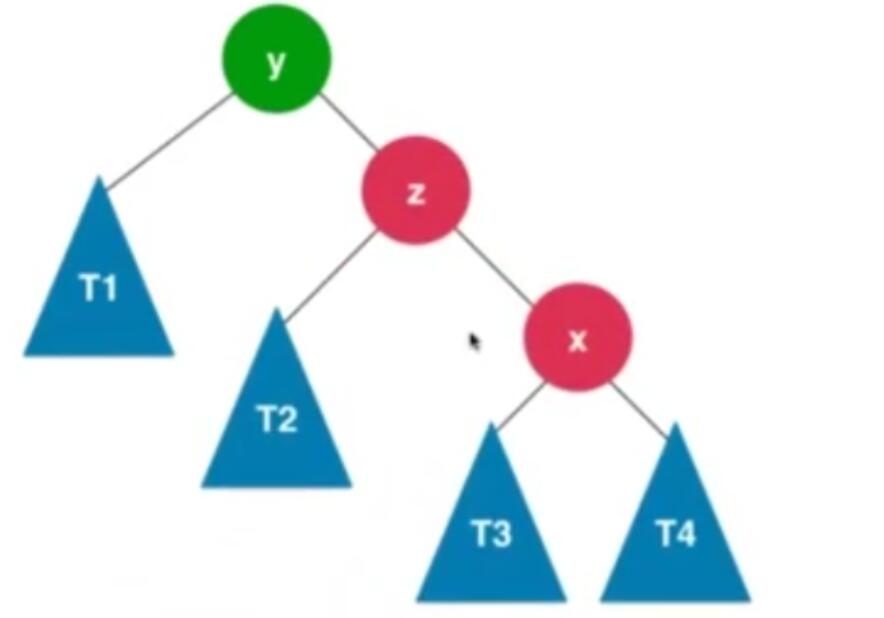
成为RR情况，对y进行左旋转

---

基于AVL树的集合和映射

AVLMap

package map;

/**
 * @author zqnh
 * @date 2019/8/5 on 20:51.
 */
public class AVLMap<K extends Comparable<K>,V> implements Map<K,V>
{
    private AVLTree<K,V> avl;
    public AVLMap()
    {
        avl = new AVLTree<>();
    }
    @Override
    public void add(K key, V value)
    {
        avl.add(key, value);
    }
    @Override
    public V remove(K key)
    {
        return null;
    }
    @Override
    public boolean contains(K key)
    {
        return avl.contains(key);
    }
    @Override
    public V get(K key)
    {
        return avl.get(key);
    }
    @Override
    public void set(K key, V newValue)
    {
        avl.set(key,newValue);
    }
    @Override
    public int getSize()
    {
        return avl.getSize();
    }
    @Override
    public boolean isEmpty()
    {
        return avl.isEmpty();
    }
}

AVLSet

package trie;

import AVL.AVLTree;

/**
 * @author zqnh
 * @date 2019/8/5 on 21:00.
 */
public class AVLSet<E extends Comparable<E>> implements Set<E>
{
    private AVLTree<E,Object> avl;
    public AVLSet()
    {
        avl = new AVLTree<>();
    }

    @Override
    public void add(E e)
    {
        avl.add(e,null);
    }

    @Override
    public void remove(E e)
    {
        avl.remove(e);
    }

    @Override
    public boolean contains(E e)
    {
        return avl.contains(e);
    }

    @Override
    public int getSize()
    {
        return avl.getSize();
    }

    @Override
    public boolean isEmpty()
    {
        return avl.isEmpty();
    }
}