数据结构之优先队列和堆

优先队列：普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

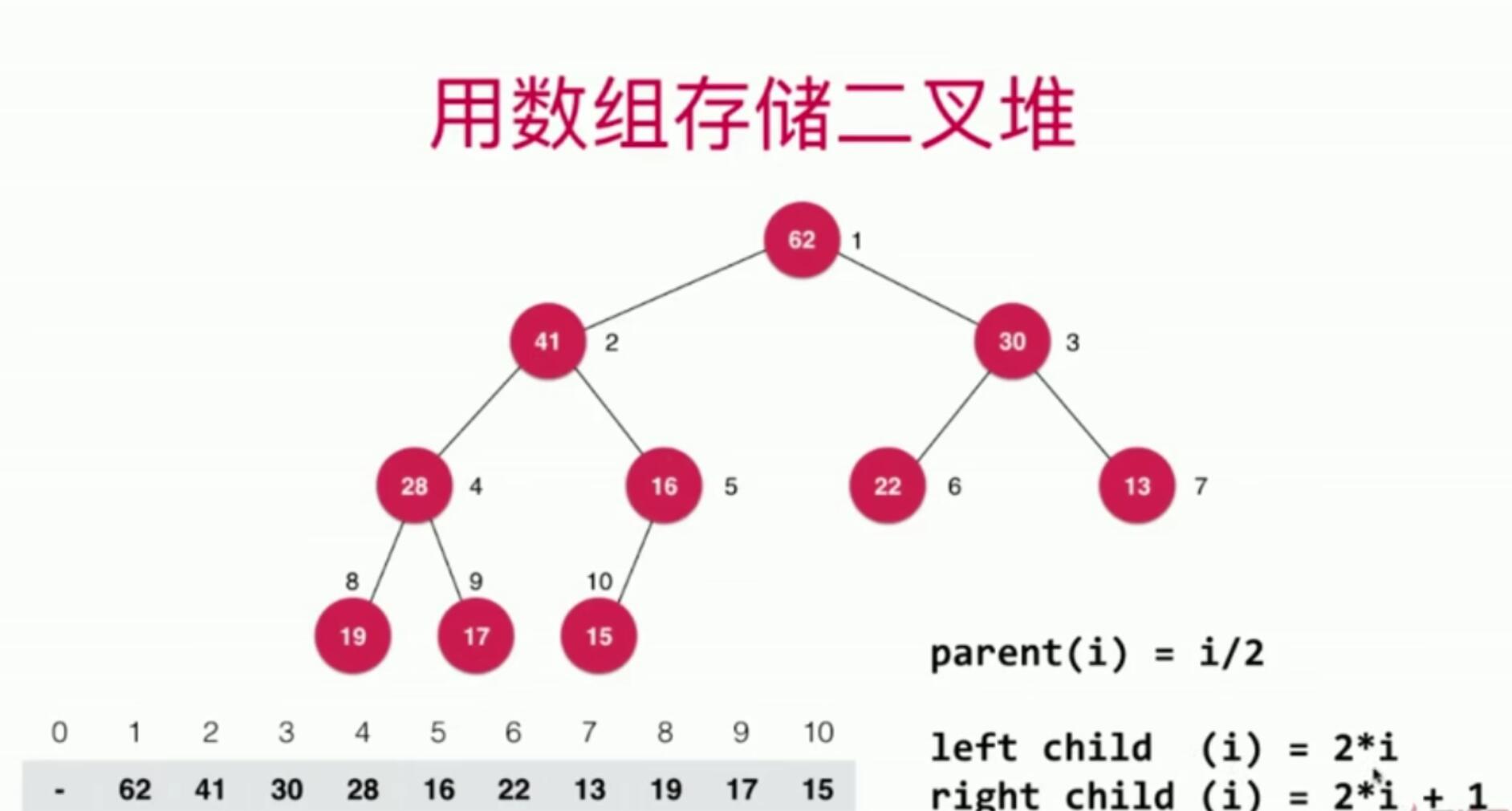
二叉堆

• 二叉堆是完全二叉树
• 堆中某个结点的值总是不大于其父节点的值

package head;
public class MaxHead<E extends Comparable<E>>
{
    private Array<E> data;
    public MaxHead(int capacity)
    {
        data = new Array<>(capacity);
    }
    public MaxHead()
    {
        data = new Array<>();
    }
    //返回堆中元素个数
    public int size()
    {
        return data.getSize();
    }
    //返回一个布尔值，表示堆中是否为空
    public boolean isEmpty()
    {
        return data.isEmpty();
    }
    //返回完全二叉树的数组表示，一个索引所表示的元素的父亲结点的索引
    private int parent(int index)
    {
        if(index == 0)
            throw new IllegalArgumentException("index-0 doesn't hava parent.");
        return (index-1)/2;
    }
    //返回完全二叉树的数组表示，一个索引所表示的元素的左孩子结点的索引
    public int leftChild(int index)
    {
        return index*2+1;
    }
    //返回完全二叉树的数组表示，一个索引所表示的元素的右孩子的结点的索引
    public int leftChild(int index)
    {
        return index*2+2;
    }
}

基于堆的优先队列

public interface Queue<E>
{
	int getSize();
	boolean isEmpty();
	void enqueue(E e);
	E dequeue();
	E getFront();
}

public class PriorityQueue<E extends Comparable<E>> implements Queue<E>
{
	private MaxHeap<E> maxHeap;
	public PriorityQueue()
	{
		max = new MaxHeap<>();
	}
	Override
	public int getSize()
	{
		return maxHeap.size();
	}
	@Override
	public boolean isEmpty()
	{
		return maxHeap.isEmpty();
	}
	@Override
	public E getFront()
	{
		return maxHeap.findMax();
	}
	@Override
	public void enqueue(E e)
	{
		maxHeap.add(e);
	}
	@Override
	public E dequeue()
	{
		return maxHeap.extractMax();
	}

}

优先队列经典问题 leecode

在1，000，000个元素选出前100名？（运用最大堆，将100个元素放入堆中，然后比较其他元素比这100个元素中最小的还大，把这个最小的替换出去）

前K个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.TreeMap;
public class Solution
{
    private class Freq implements Comparable<Freq>
    {
        int e,freq;
        public Freq(int e,int freq)
        {
            this.e = e;
            this.freq = freq;
        }
        @Override
        public int compareTo(Freq another)
        {
            if(this.freq<another.freq)
                return -1;
            else if(this.freq>another.freq)
                return 1;
            else
                return 0;
        }
    }
    public List<Integer> topKFrequent(int[] nums, int k)
    {

        TreeMap<Integer,Integer> map = new TreeMap<>();
        for (int num:nums)
        {
            if(map.containsKey(num))
                map.put(num,map.get(num)+1);
            else
                map.put(num,1);
        }
        PriorityQueue<Freq> pq = new PriorityQueue<>();
        for(int key:map.keySet())
        {
            if(pq.size()<k)
                pq.add(new Freq(key,map.get(key)));
            else if(map.get(key)>pq.peek().freq)
            {
                pq.remove();
                pq.add(new Freq(key,map.get(key)));
            }
        }
        LinkedList<Integer> res = new LinkedList<>();
        while(!pq.isEmpty())
            res.add(pq.remove().e);
        return res;
    }
}